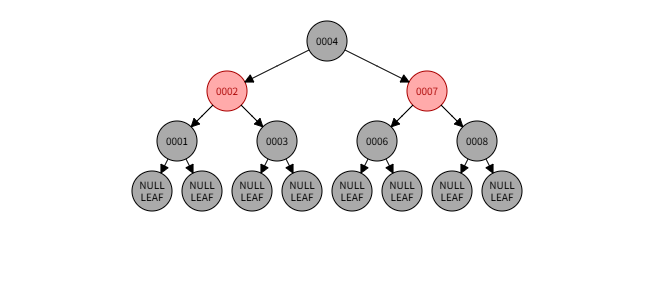
相关名词整理
发现之前的逻辑有点不对,重新整理一份
树
树是由节点(Node)和边(Edge)组成的有限集合,满足以下条件:
- 根节点(Root):存在且仅存在一个特定的节点,称为树的根节点。
- 子节点与父节点:除根节点外,每个节点通过一条边唯一地连接到一个称为其父节点的节点。
- 子树(Subtree):每个节点可以有零个或多个子节点,子节点对应的子树是互不相交的集合。
- 无环性:树中不存在环路(即从任一节点出发沿着边遍历,无法回到该节点)。
- 连通性:所有节点通过边连接,且从根节点出发可通过边到达任意其他节点。
二叉树
首先,二叉树是树
二叉树是由节点(Node)构成的有限集合,满足以下条件:
- 节点结构:每个节点最多有两个子节点,分别称为左子节点(Left Child)和右子节点(Right Child)。
- 子树性质:左子节点和右子节点各自构成一个独立的二叉树(可以为空树)。
- 根节点:存在且仅存在一个根节点(若二叉树非空)。
- 无环与连通性:与普通树一致,二叉树中不存在环路,且所有节点通过边与根节点连通。
平衡树
B-Tree,又称B树,B-树,定义如下
- 每个节点最多包含 m−1 个键(Key),最少包含 ⌈m/2⌉−1 个键(根节点和叶子节点可能有例外)。
- 每个节点最多有 m 个子节点(m 是 B树的阶,通常取值≥3)。
- 键的作用:数据按顺序排列,同时起到索引作用,用于路由查询路径。
二叉平衡树
即AVL,详解可以见这里
红黑树
AVL固然很好,但是因为增加元素/节点的时候很容易去修改整个树的结构,因为AVL很强调树的平衡性。
如果频繁修改树结构的话,业务开销的占比就会降低了,固然是我们不希望看到的。
但又同时:树的平衡和查找开销低的特点我们都想要,那么红黑树就是满足这个条件的一个解决方案
红黑树是一种自平衡的二叉搜索树,通过以下五个性质确保高效的操作时间复杂度(O(log n)):
- 颜色属性:每个节点必须是红色或黑色。
- 根节点属性:根节点必须为黑色。
- 叶子节点属性:所有叶子节点(NIL节点,即空节点)均为黑色。
- 红色节点约束:红色节点的子节点必须为黑色(即不存在两个连续的红色节点)。
- 黑高一致性:从任一节点到其所有后代叶子节点的路径上,包含相同数量的黑色节点(称为黑高)。
并且包含一些规则
- 节点分为红色或者黑色;
- 根节点必为黑色;
- 叶子节点都为黑色,且为null;
- 连接红色节点的两个子节点都为黑色(红黑树不会出现相邻的红色节点,可以出现相邻的黑色节点);
- 从任意节点出发,到其每个叶子节点的路径中包含相同数量的黑色节点;
- 新加入到红黑树的节点为红色节点;
结合图理解

下图是红黑树吗?
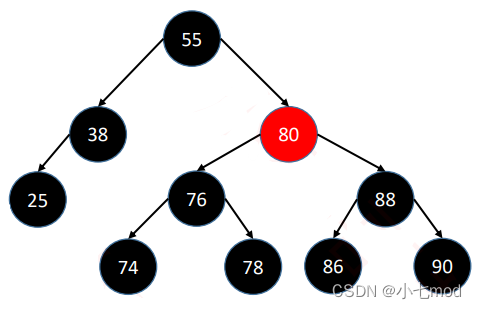
不是,因为不满足条件黑高一致性
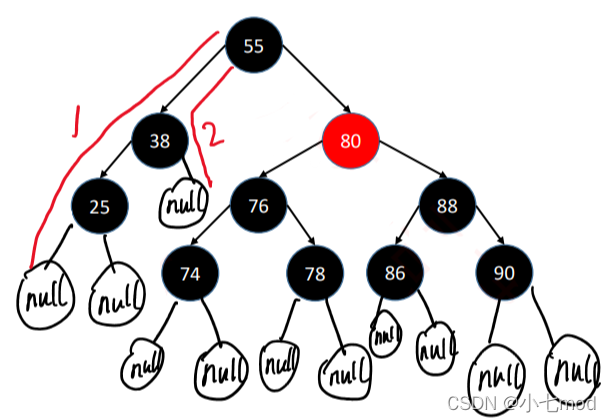
增删改查
聚焦于增和删
增
情况一:
插入的新节点 N 是红黑树的根节点,这种情况下,我们把节点 N 的颜色由红色变为黑色,性质2(根是黑色)被满足。同时 N 被染成黑色后,红黑树所有路径上的黑色节点数量增加一个,性质5(从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点)仍然被满足。

情况二:
N 的父节点是黑色,这种情况下,性质4(每个红色节点必须有两个黑色的子节点)和性质5没有受到影响,不需要调整。
情况三,四,五比较复杂,没耐心的直接看最后的对比图
情况三:
N 的父节点是红色(节点 P 为红色,其父节点必然为黑色),叔叔节点 U 也是红色。由于 P 和 N 均为红色,所有性质4被打破,此时需要进行调整。
这种情况下,先将 P 和 U 的颜色染成黑色,再将 G 的颜色染成红色。此时经过 G 的路径上的黑色节点数量不变,性质5仍然满足。但需要注意的是 G 被染成红色后,可能会和它的父节点形成连续的红色节点,此时需要递归向上调整。
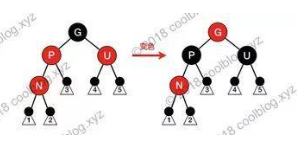
情况四:
N 的父节点为红色,叔叔节点为黑色。节点 N 是 P 的右孩子,且节点 P 是 G 的左孩子。此时先对节点 P 进行左旋,调整 N 与 P 的位置。接下来按照情况五进行处理,以恢复性质4。
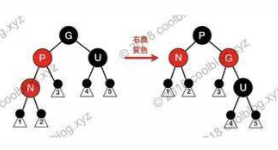
情况五:
N 的父节点为红色,叔叔节点为黑色。N 是 P 的左孩子,且节点 P 是 G 的左孩子。此时对 G 进行右旋,调整 P 和 G 的位置,并互换颜色。经过这样的调整后,性质4被恢复,同时也未破坏性质5。
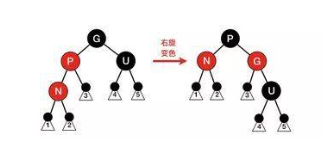
上面五种情况中,情况一和情况二比较简单,情况三、四、五稍复杂。但如果细心观察,会发现这三种情况的区别在于叔叔节点的颜色,如果叔叔节点为红色,直接变色即可。如果叔叔节点为黑色,则需要先选择,再交换颜色。当把这三种情况的图画在一起就区别就比较容易观察了,如下图:
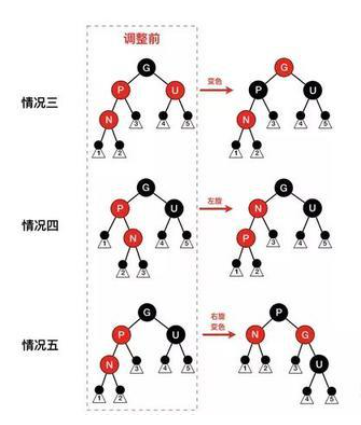
其他的就是对称操作了
删
红黑树删除操作的复杂度在于删除对象的各种排列组合的情况复杂多样,但是可以通过理论来进行缩减
按照二叉搜索树(BST)规则删除节点:
- 无子节点:直接删除。
- 一个子节点:用子节点替代。
- 两个子节点:用后继节点替代,转为删除后继节点。
如果被删除节点存在两个子节点,那么红黑树会将后继节点的数据复制到被删除节点的位置,仅覆盖数据值,不改变被删除节点的颜色或指针
那么此时,等于删除了后继节点,故 删除节点有两个子节点 == 删除后继结点
从数据上看确实是删除了需要删除的节点,但是红黑树关注的是树结构,颜色是否都符合红黑树规则,所以对于红黑树来说,删除的数据不重要,只有结构和规则不匹配才重要。
又因为后继结点最多只有一个子节点,故 删除后继结点 == 删除一个子节点/无子节点
后继节点按照BST右树最小元素来看:
若节点 x 有右子树,则其后继节点为右子树的最左节点。
由于该节点是右子树中的“最左”节点,它不可能有左子节点(否则会更小的节点存在,与其“最左”矛盾)。因此,该后继节点最多仅有一个右子节点,或无子节点。
所以 删除节点有两个子节点 == 删除后继结点 == 删除一个子节点/无子节点
所以情况就变成了两种情况
那么此时,所有的情况就变成了四种,只有一种情况需要重点考虑
| 所有的情况 |
被删除节点为红色 |
被删除节点为黑色 |
| 被删除节点为无子节点 |
直接删除即可 |
复杂处理,见下 |
| 被删除节点有一个子节点 |
不存在
该结构的出现不满足红黑树黑高一致性 |
子节点必为红色,否则违反黑高一致性
修复方法为:子红节点替换被删除黑节点,颜色变为黑色 |
被删除节点为黑色且被删除节点无子节点,需要进行复杂处理,可能的情况如下
被删除节点为根节点:直接删除,红黑树转空树
如果被删除节点 D 为叶子节点且被删除节点无子节点,观察:
-
兄弟节点 B 为红色,其子节点必为黑色(性质4)。父节点 P 为黑色
修复:
1.1)将父节点 P 染为红色,兄弟节点 B 染为黑色。
1.2)对父节点 P 进行左旋(若兄弟在右侧)或右旋(若兄弟在左侧)。
1.3)此时,原兄弟的子节点 L/R 成为新的兄弟节点(必为黑色),进入 情况2、3、4 继续处理。
1)例子:删除005
1)删除过程:
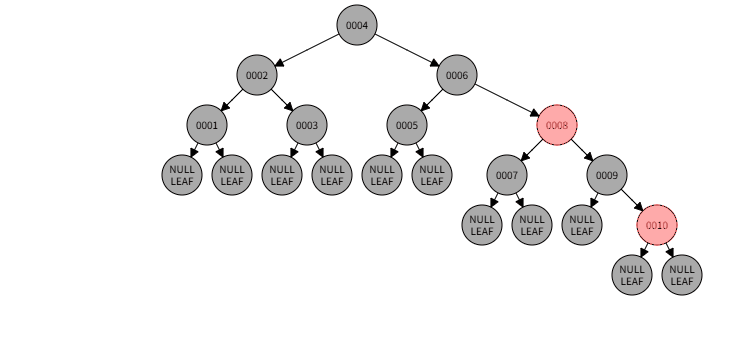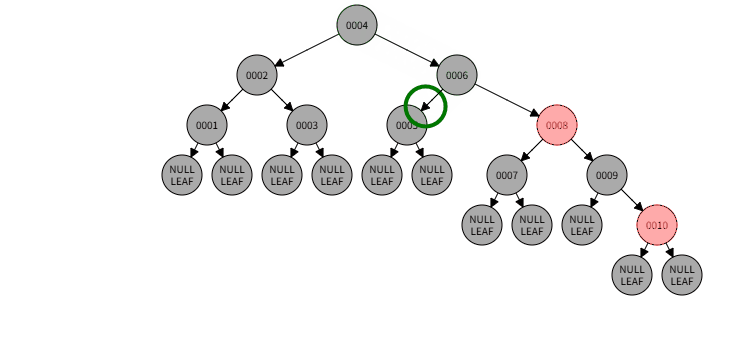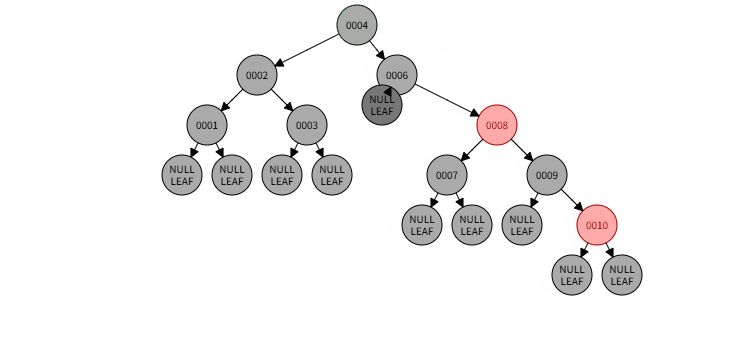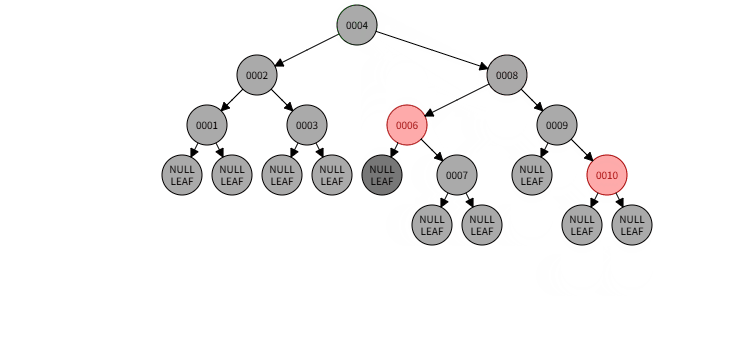
1)本情况处理结果:
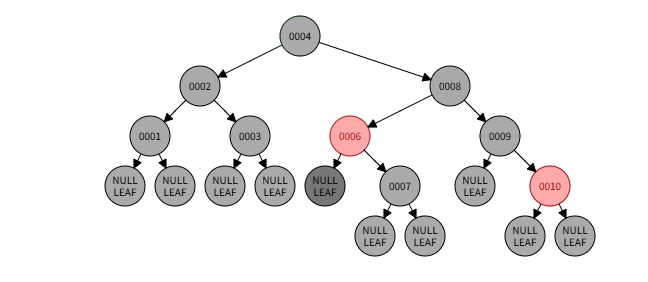
(例子后续接情况2,此时以深色黑色 NULL LEAF作为参考)
-
兄弟节点是黑色,且其子节点均为黑色
修复:
2.1)将兄弟节点 S 染为红色。
2.2)若父节点P为红色:
2.2)例子:删除 001
2.2)删除过程:
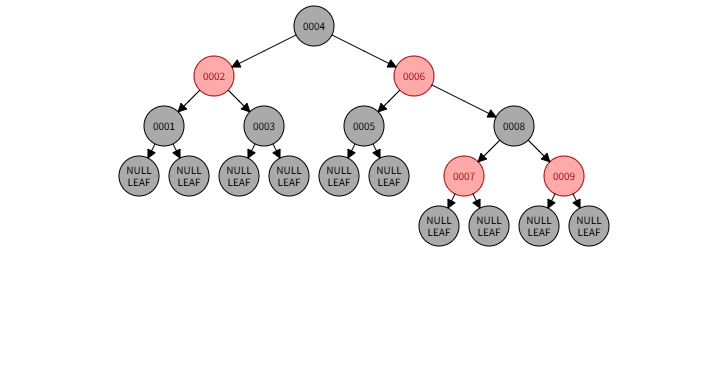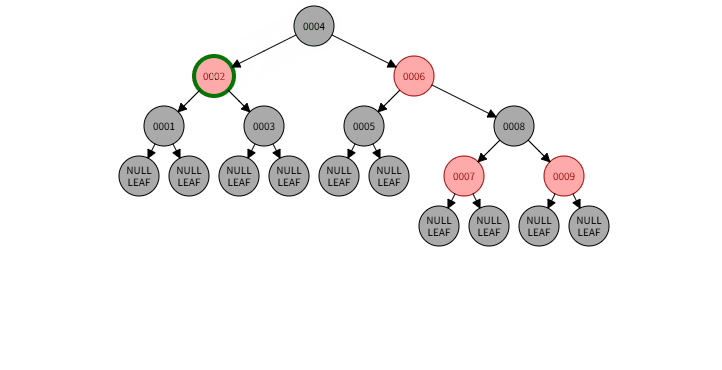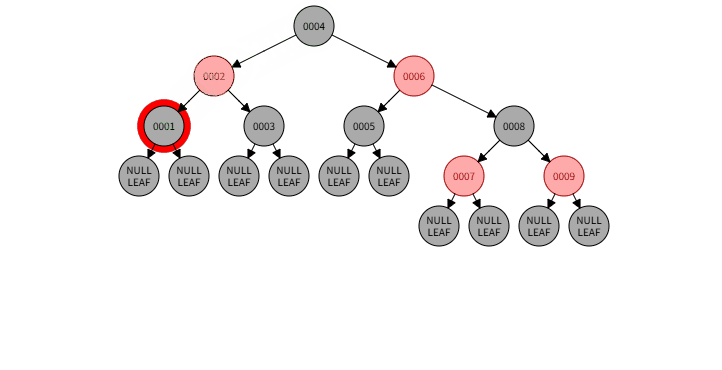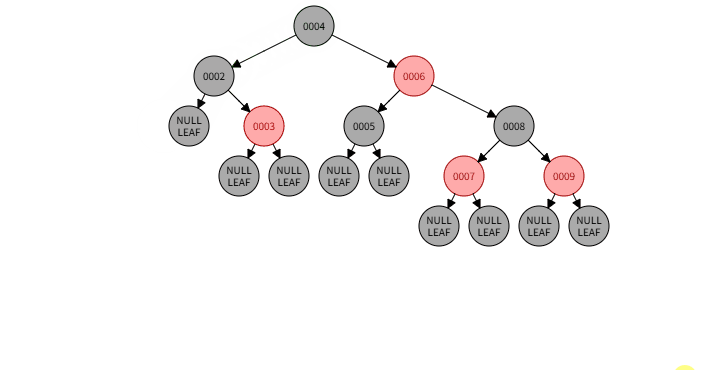
2.2)本情况处理结果:
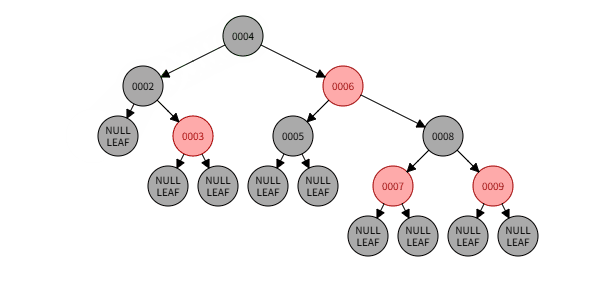
2.3)若父节点P为黑色:
- 将 P 视为新的删除位置,递归向上处理(可能进入情况1、2、3、4)。
2.3)例子:删除001
2.3)删除过程:
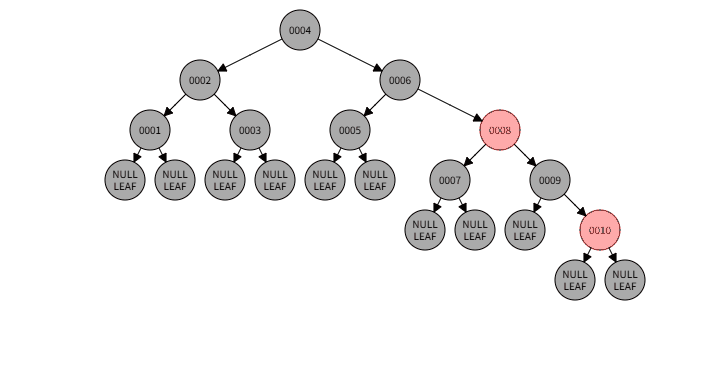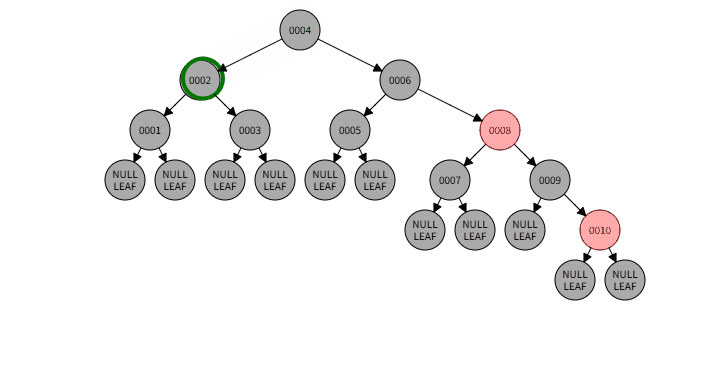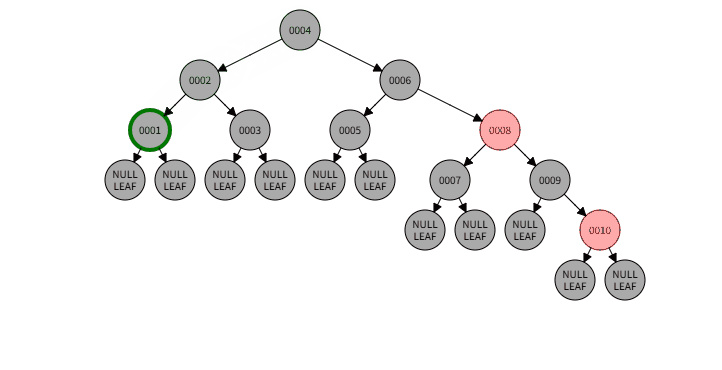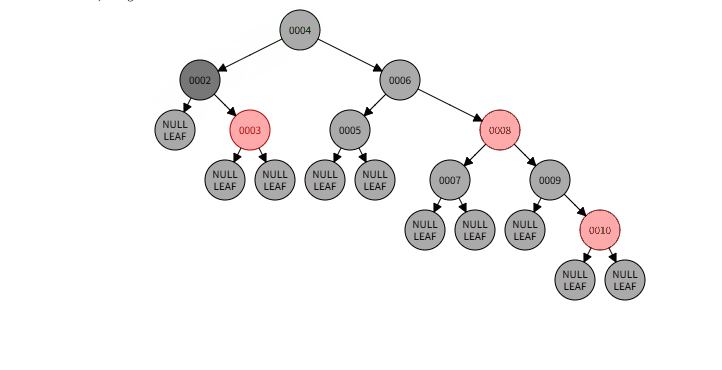
2.3)本情况处理结果:
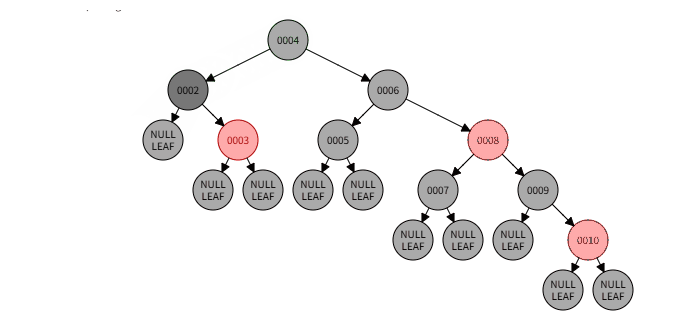
-
兄弟节点是黑色,且近侄子节点为红色,远侄子节点为黑色
修复:
3.1)将兄弟节点 S 染为红色,近侄子 C 染为黑色。
3.2)对兄弟节点 S 进行左旋(若兄弟在左侧)。
3.3)此时远侄子 D 成为新的兄弟节点,进入 情况4。
3)例子:删除0013
3)删除过程:
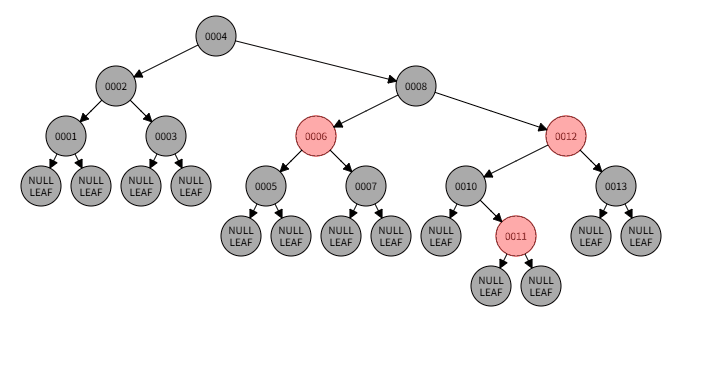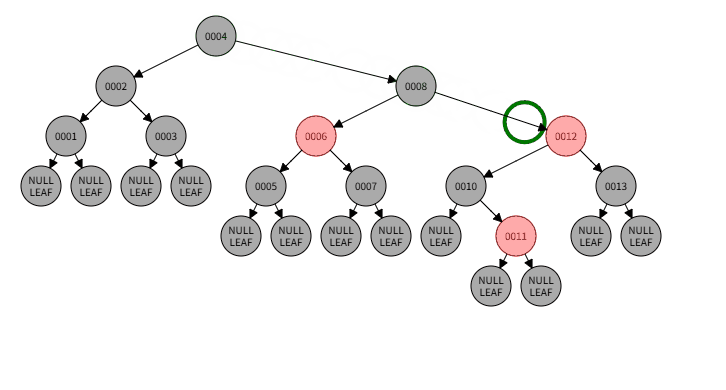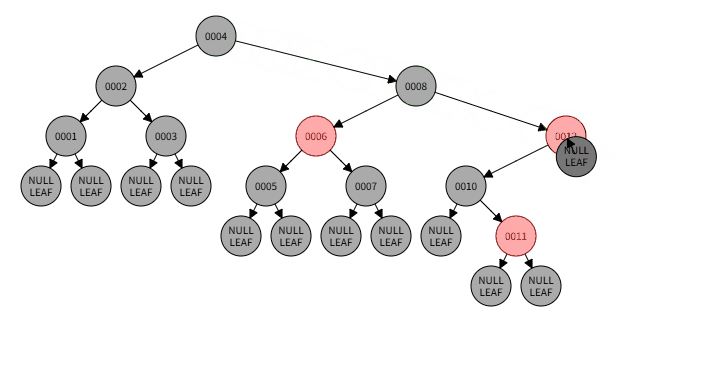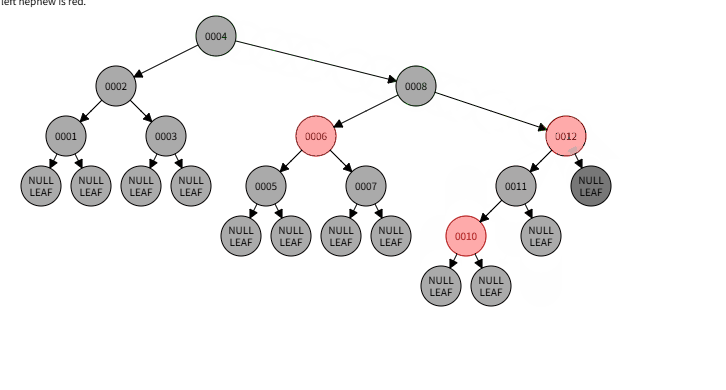
3)本情况处理结果:
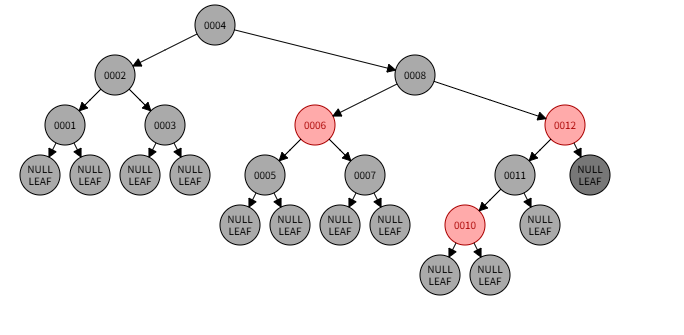
-
兄弟节点是黑色,且远侄子节点为红色
修复:
4)对父节点 P 进行左旋(若兄弟在右侧)。
4)将兄弟节点 S 染为父节点 P 的颜色。
4)将父节点 P 染为黑色,远侄子 D 染为黑色。
4)修复完成:旋转后,删除路径的黑色高度恢复,且无连续红色节点。
4)例子:删除009
4)删除过程:
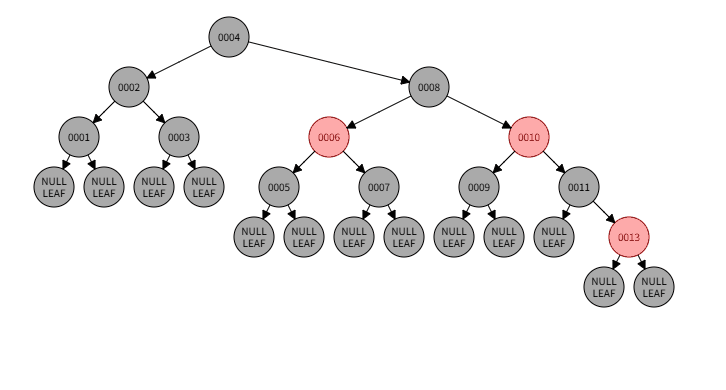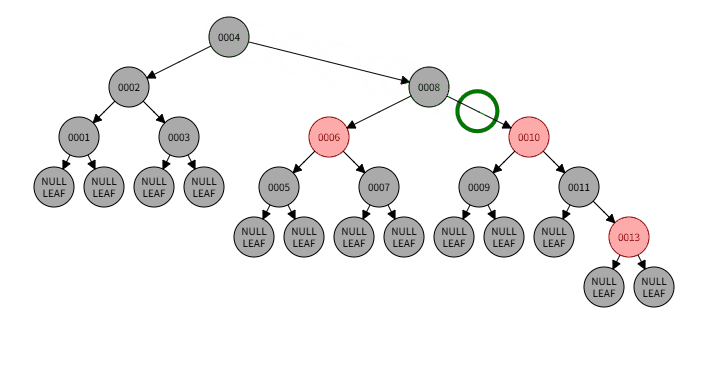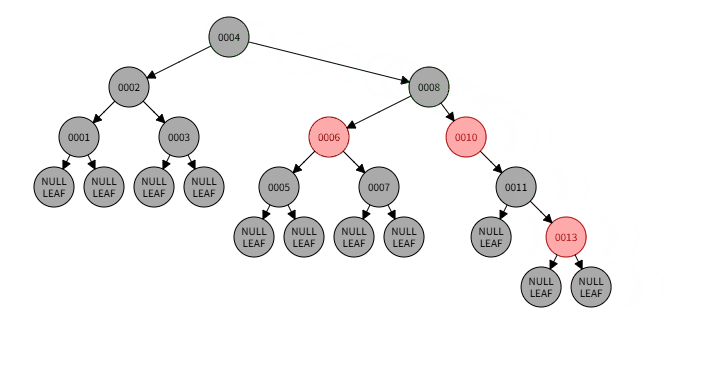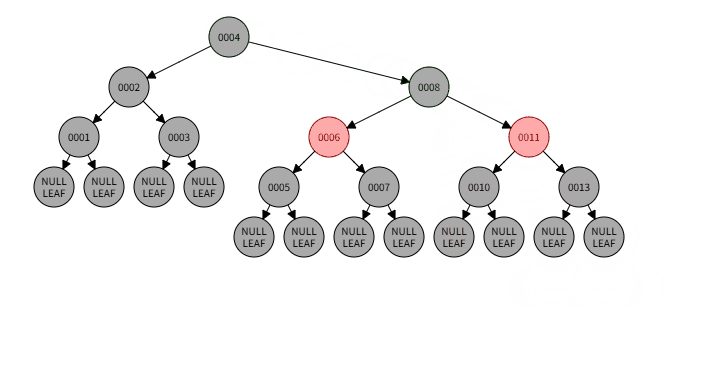
4)本情况处理结果:
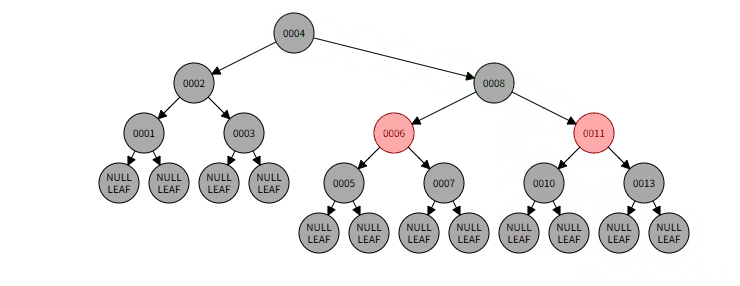
删的情况到此结束了
如果没有看懂的话,可以进入这个网站,结合所写情况一步步调试查看即可
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
|
import os
from graphviz import Digraph
os.environ["PATH"] += os.pathsep + r'D:\Program Files\Graphviz\bin'
class RBNode:
def __init__(self, key, value=None, color='RED'):
self.key = key
self.value = value
self.left = None
self.right = None
self.parent = None
self.color = color # RED/BLACK
class RedBlackTree:
def __init__(self):
self.NIL = RBNode(None, color='BLACK') # 哨兵节点
self.root = self.NIL
def left_rotate(self, x):
""" 左旋操作 """
y = x.right
x.right = y.left
if y.left != self.NIL:
y.left.parent = x
y.parent = x.parent
if x.parent == self.NIL:
self.root = y
elif x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
def right_rotate(self, y):
""" 右旋操作 """
x = y.left
y.left = x.right
if x.right != self.NIL:
x.right.parent = y
x.parent = y.parent
if y.parent == self.NIL:
self.root = x
elif y == y.parent.right:
y.parent.right = x
else:
y.parent.left = x
x.right = y
y.parent = x
def insert(self, key, value=None):
""" 插入主逻辑 """
new_node = RBNode(key, value)
new_node.left = self.NIL
new_node.right = self.NIL
# 标准BST插入
parent = self.NIL
current = self.root
while current != self.NIL:
parent = current
if new_node.key < current.key:
current = current.left
else:
current = current.right
new_node.parent = parent
if parent == self.NIL:
self.root = new_node
elif new_node.key < parent.key:
parent.left = new_node
else:
parent.right = new_node
# 修正红黑树性质
self._insert_fixup(new_node)
def _insert_fixup(self, node):
""" 插入后修正颜色和旋转 """
while node.parent.color == 'RED':
if node.parent == node.parent.parent.left:
uncle = node.parent.parent.right
if uncle.color == 'RED':
# Case 1: 叔叔是红色
node.parent.color = 'BLACK'
uncle.color = 'BLACK'
node.parent.parent.color = 'RED'
node = node.parent.parent
else:
if node == node.parent.right:
# Case 2: 叔叔是黑色且当前节点是右子
node = node.parent
self.left_rotate(node)
# Case 3: 叔叔是黑色且当前节点是左子
node.parent.color = 'BLACK'
node.parent.parent.color = 'RED'
self.right_rotate(node.parent.parent)
else:
uncle = node.parent.parent.left
if uncle.color == 'RED':
node.parent.color = 'BLACK'
uncle.color = 'BLACK'
node.parent.parent.color = 'RED'
node = node.parent.parent
else:
if node == node.parent.left:
node = node.parent
self.right_rotate(node)
node.parent.color = 'BLACK'
node.parent.parent.color = 'RED'
self.left_rotate(node.parent.parent)
if node == self.root:
break
self.root.color = 'BLACK'
def visualize(self, filename='rbtree'):
""" 生成可视化图形 """
dot = Digraph(comment='Red Black Tree')
self._add_nodes(dot, self.root)
dot.render(filename, view=True, format='png')
# dot.view()
# os.remove(filename) # 清理临时文件
def _add_nodes(self, dot, node):
""" 递归添加节点和边 """
if node == self.NIL:
return
dot.node(str(node.key), f"{node.key}\n{node.color}",
shape='circle',
color='red' if node.color == 'RED' else 'black',
fontcolor='white' if node.color == 'BLACK' else 'black',
style='filled')
if node.left != self.NIL:
dot.edge(str(node.key), str(node.left.key))
self._add_nodes(dot, node.left)
if node.right != self.NIL:
dot.edge(str(node.key), str(node.right.key))
self._add_nodes(dot, node.right)
# 测试示例
if __name__ == "__main__":
rbt = RedBlackTree()
keys = [7, 3, 18, 10, 22, 8, 11, 26]
for k in keys:
rbt.insert(k)
rbt.visualize()
|
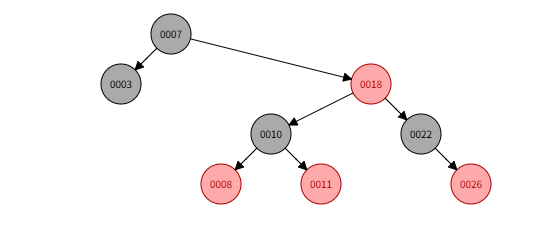
Ref
https://blog.csdn.net/cy973071263/article/details/122543826
https://zhuanlan.zhihu.com/p/91960960