因为看java内部库实现的时候，没看出来一些典型的算法，补补课相当于

~~别问为什么用python实现~~

二叉查找树

Binary Search Tree => BST

二叉查找树根节点的值大于其左子树中任意一个节点的值，小于其右子树中任意一节点的值，且该规则适用于树中的每一个节点。

二叉查找树的查询效率介于O(log n)~O(n)之间，理想的排序情况下查询效率为O(log n),极端情况下BST就是一个链表结构(如下图)，此时元素查找的效率相等于链表查询O(n)。

BST 增删改查

不考虑其他情况（BST的查找性能或其他时），仅考虑增加元素时的增删改查

增

空树的情况：当BST为空时，新插入的节点成为根节点。
插入到左子树或右子树的叶子节点位置：例如，当前节点有左子树为空，且新键小于当前节点键，则新节点作为左子节点插入。
递归遍历到适当的位置：在非叶子节点的情况下，需要继续向下遍历左或右子树，直到找到空的位置。
重复键的处理：可能需要返回错误或者忽略，或者根据需求处理。

删

删除叶子节点：这是最简单的情况，直接删除即可，不影响其他节点。
删除有一个子节点的节点：需要将父节点的指针指向被删除节点的子节点，保持BST的有序性。
删除有两个子节点的节点：这种情况最复杂，需要找到合适的替换节点（通常是左子树的最大值或右子树的最小值），然后递归删除替换节点，以避免破坏BST的结构。
删除节点不存在：返回原BST即可。

改

修改后的键值与原键值相同：这种情况下，实际上不需要做任何修改，因为键值没有变化。但如果是修改与键关联的数据（如值或附加信息），则可以直接更新数据部分，不影响树的结构。
修改后的键值不改变其在树中的位置：新键值仍然位于原节点的父节点和子节点之间，即新键值仍然满足原父节点的左子树或右子树的条件，以及其子节点的条件。只要满足：
1. 大于左子树的最大键值且小于右子树的最小键值
2. 父节点约束（若存在父节点）：
  - 若当前节点是父节点的左子节点，新键值 < 父节点键值。
  - 若当前节点是父节点的右子节点，新键值 > 父节点键值。
此时，无需调整树结构。
修改后的键值破坏了BST的有序性，需要调整树结构：这是更复杂的情况。例如，将某个节点的键值修改为比其左子树的某个节点小，或比其右子树的某个节点大，导致无法维持BST的性质。此时，必须删除原节点，然后插入新的键值，以确保整个树的有序性。删和增参考之前的描述操作

查

就是简单的对比查找即可，不存在返回空

平衡二叉查找树

在BST的模式下，如果按照默认插入方式，极端情况下可能会造成BST退化为链表的状态

所以，需要解决如下问题：

我何时知道我的 BST 变成了 “不好” 的状态；（根据什么规则可以确定我的BST退化了？）
我如何调整我的 BST ，使其达到可接受的平衡状态

为了防止BST的退化，或找到最适合业务，最快的查询树是需要满足什么条件？什么样的树是平衡的，不是退化的？于是AVL被提出。

Balanced Binary Search Tree => AVL

AVL 是大学教授 G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写，他们提出的平衡二叉树的概念，为了纪念他们，将平衡二叉树称为 AVL树。

AVL树本质上是一颗二叉查找树，但是它又具有以下特点：

它是一棵空树 or 它的左右两个子树的高度差的绝对值不超过1，
左右两个子树也都是一棵AVL树。

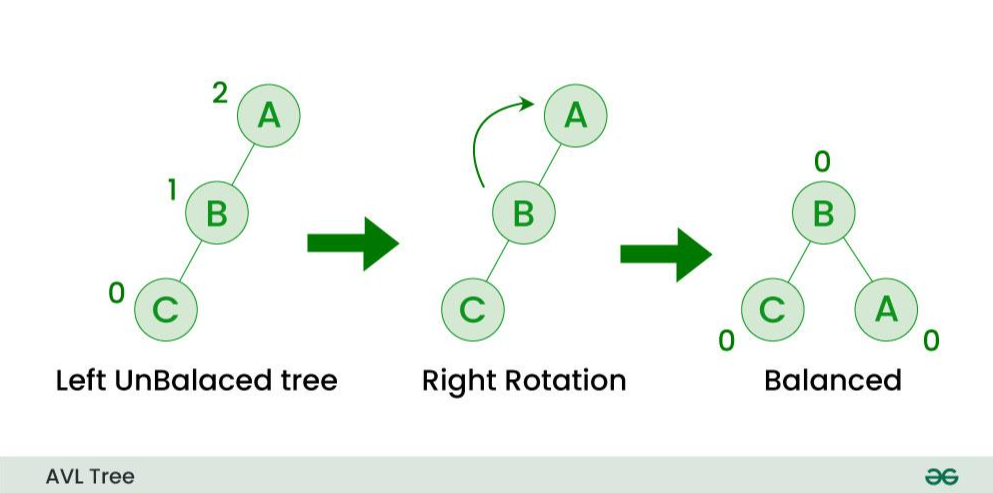
AVL树判断是否平衡的标志，引入了平衡因子的概念（Balance Factor，简写为BF）

平衡因子（BF）：结点的左子树的深度减去右子树的深度。

即： 结点的平衡因子 = 左子树的高度 - 右子树的高度 。

图示：

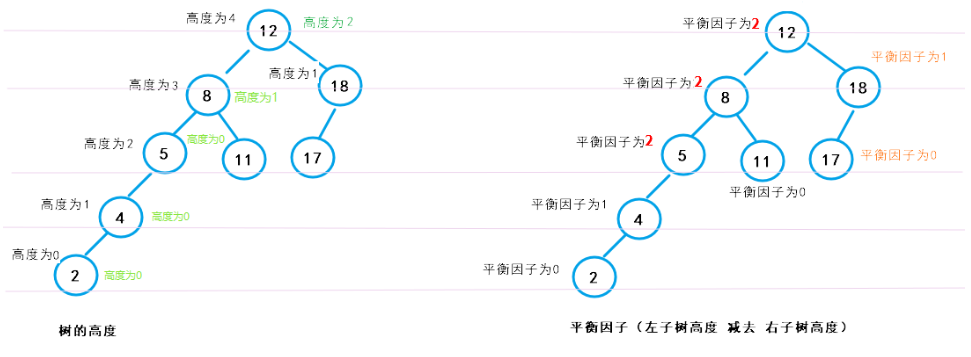
分别计算当前节点的左最高高度和右最高高度，差为BF

在 AVL树中，所有节点的平衡因子都必须满足： |bf|<=1;

AVL 增删改查

AVL 的查操作与BST一样，改操作可能有直接修改键值并局部调整的算法，但工业级实现（如标准库）普遍采用删增分解策略，所以我们的目光放在增和删上

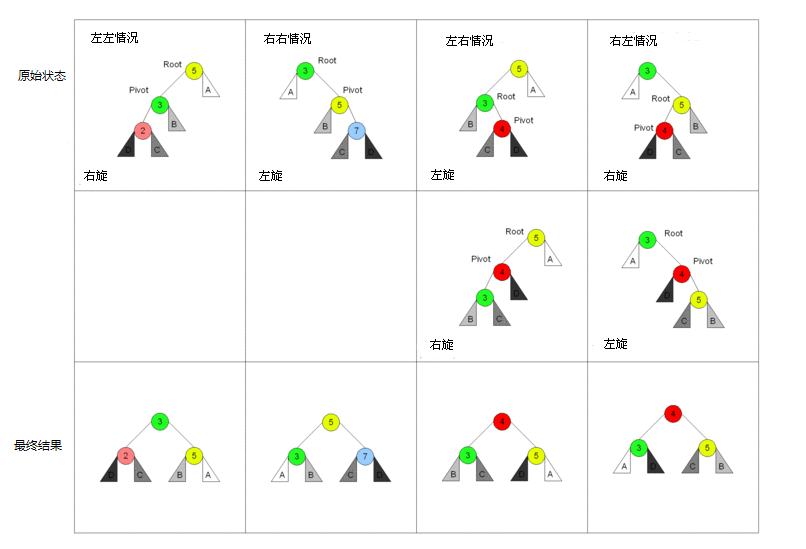
增

https://blog.csdn.net/xiaojin21cen/article/details/97602146

没错，不重复造轮子，这个文章写的很好了已经

贴个总结，纯黑是插入的节点

删

按照BST删的方式进行删除后，从子节点开始计算BF，重新进行左旋右旋操作即可

代码

BST

带可视化输出：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82


class TreeNode:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key

class BST:
    def __init__(self):
        self.root = None

    def insert(self, root, key):
        if not root:
            return TreeNode(key)
        if key < root.val:
            root.left = self.insert(root.left, key)
        else:
            root.right = self.insert(root.right, key)
        return root

    def delete(self, root, key):
        if not root:
            return root
        if key < root.val:
            root.left = self.delete(root.left, key)
        elif key > root.val:
            root.right = self.delete(root.right, key)
        else:
            if not root.left:
                return root.right
            elif not root.right:
                return root.left
            temp = self.getMinValueNode(root.right)
            root.val = temp.val
            root.right = self.delete(root.right, temp.val)
        return root

    def getMinValueNode(self, root):
        current = root
        while current.left:
            current = current.left
        return current

    def search(self, root, key):
        if not root or root.val == key:
            return root
        if key < root.val:
            return self.search(root.left, key)
        return self.search(root.right, key)

    def update(self, root, old_key, new_key):
        self.delete(root, old_key)
        self.insert(root, new_key)

def print_tree_vertical(root, prefix="", is_left=True):
    if root is not None:
        print_tree_vertical(root.right, prefix + ("│   " if is_left else "    "), False)
        print(prefix + ("└── " if is_left else "┌── ") + str(root.val))
        print_tree_vertical(root.left, prefix + ("    " if is_left else "│   "), True)

# Example usage:
bst = BST()
operations = [
    (bst.insert, 50), (bst.insert, 30), (bst.insert, 70),
    (bst.insert, 20), (bst.insert, 40), (bst.insert, 80),
     (bst.insert, 130),(bst.insert, 100), (bst.insert, 120), (bst.insert, 90),
    (bst.insert, 110),(bst.insert, 150),(bst.insert, 140),(bst.insert, 160),(bst.insert, 139),
    (bst.delete, 130), (bst.update, (70, 60)), (bst.search, 50)
]

for operation, value in operations:
    if operation == bst.search:
        result = bst.search(bst.root, value)
        print(f"Search {value} -> Found: {result.val if result else 'Not Found'}")
    elif operation == bst.update:
        old_key, new_key = value[0], value[1]
        bst.update(bst.root, old_key, new_key)
        print(f"Update {old_key} -> {new_key}")
    else:
        bst.root = operation(bst.root, value)
        print(f"After {operation.__name__} {value}:")
        print_tree_vertical(bst.root)
        print("-" * 50)  # Separator for clarity

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52


--------------------------------------------------
After insert 160:
│                   ┌── 160
│               ┌── 150
│               │   └── 140
│           ┌── 130
│           │   │   ┌── 120
│           │   │   │   └── 110
│           │   └── 100
│           │       └── 90
│       ┌── 80
│   ┌── 70
└── 50
    │   ┌── 40
    └── 30
        └── 20
--------------------------------------------------
After insert 139:
│                   ┌── 160
│               ┌── 150
│               │   └── 140
│               │       └── 139
│           ┌── 130
│           │   │   ┌── 120
│           │   │   │   └── 110
│           │   └── 100
│           │       └── 90
│       ┌── 80
│   ┌── 70
└── 50
    │   ┌── 40
    └── 30
        └── 20
--------------------------------------------------
After delete 130:
│                   ┌── 160
│               ┌── 150
│               │   └── 140
│           ┌── 139
│           │   │   ┌── 120
│           │   │   │   └── 110
│           │   └── 100
│           │       └── 90
│       ┌── 80
│   ┌── 70
└── 50
    │   ┌── 40
    └── 30
        └── 20
--------------------------------------------------
Update 70 -> 60
Search 50 -> Found: 50

AVL

同样带可视化输出

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147


class TreeNode:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.height = 1

class AVLTree:
    def get_height(self, node):
        return node.height if node else 0

    def get_balance(self, node):
        return self.get_height(node.left) - self.get_height(node.right) if node else 0

    def update_height(self, node):
        node.height = 1 + max(self.get_height(node.left), self.get_height(node.right))

    def rotate_right(self, y):
        x = y.left
        T2 = x.right
        x.right = y
        y.left = T2
        self.update_height(y)
        self.update_height(x)
        return x

    def rotate_left(self, x):
        y = x.right
        T2 = y.left
        y.left = x
        x.right = T2
        self.update_height(x)
        self.update_height(y)
        return y

    def insert(self, node, key):
        if not node:
            return TreeNode(key)
        if key < node.key:
            node.left = self.insert(node.left, key)
        elif key > node.key:
            node.right = self.insert(node.right, key)
        else:
            return node  # Duplicate keys not allowed

        self.update_height(node)
        balance = self.get_balance(node)

        # Left Left Case
        if balance > 1 and key < node.left.key:
            return self.rotate_right(node)
        # Right Right Case
        if balance < -1 and key > node.right.key:
            return self.rotate_left(node)
        # Left Right Case
        if balance > 1 and key > node.left.key:
            node.left = self.rotate_left(node.left)
            return self.rotate_right(node)
        # Right Left Case
        if balance < -1 and key < node.right.key:
            node.right = self.rotate_right(node.right)
            return self.rotate_left(node)

        return node

    def find_min_value_node(self, node):
        current = node
        while current.left:
            current = current.left
        return current

    def delete(self, root, key):
        if not root:
            return root
        if key < root.key:
            root.left = self.delete(root.left, key)
        elif key > root.key:
            root.right = self.delete(root.right, key)
        else:
            if not root.left:
                return root.right
            elif not root.right:
                return root.left
            temp = self.find_min_value_node(root.right)
            root.key = temp.key
            root.right = self.delete(root.right, temp.key)

        if not root:
            return root

        self.update_height(root)
        balance = self.get_balance(root)

        # Left Left Case
        if balance > 1 and self.get_balance(root.left) >= 0:
            return self.rotate_right(root)
        # Left Right Case
        if balance > 1 and self.get_balance(root.left) < 0:
            root.left = self.rotate_left(root.left)
            return self.rotate_right(root)
        # Right Right Case
        if balance < -1 and self.get_balance(root.right) <= 0:
            return self.rotate_left(root)
        # Right Left Case
        if balance < -1 and self.get_balance(root.right) > 0:
            root.right = self.rotate_right(root.right)
            return self.rotate_left(root)

        return root

    def search(self, root, key):
        if not root or root.key == key:
            return root
        if key < root.key:
            return self.search(root.left, key)
        return self.search(root.right, key)

    def visualize(self, node, prefix="", is_left=True):
        if not node:
            return
        if node.right:
            self.visualize(node.right, prefix + ("│   " if is_left else "    "), False)
        print(prefix + ("└── " if is_left else "┌── ") + str(node.key))
        if node.left:
            self.visualize(node.left, prefix + ("    " if is_left else "│   "), True)


avl = AVLTree()
root = None
keys = [10, 20, 30, 40, 50, 25, 35, 60, 70]

print("Inserting keys into AVL Tree:")
for key in keys:
    root = avl.insert(root, key)
    print(f"\nAfter inserting {key}:")
    avl.visualize(root)

print("\nDeleting key 35 from AVL Tree:")
root = avl.delete(root, 35)
avl.visualize(root)

print("\nSearching for key 40 in AVL Tree:")
result = avl.search(root, 40)
if result:
    print(f"Key 40 found in the tree.")
else:
    print(f"Key 40 not found in the tree.")

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


After inserting 60:
│           ┌── 60
│       ┌── 50
│   ┌── 40
│   │   └── 35
└── 30
    │   ┌── 25
    └── 20
        └── 10

After inserting 70:
│           ┌── 70
│       ┌── 60
│       │   └── 50
│   ┌── 40
│   │   └── 35
└── 30
    │   ┌── 25
    └── 20
        └── 10

Deleting key 30 from AVL Tree:
│       ┌── 70
│   ┌── 60
│   │   │   ┌── 50
│   │   └── 40
└── 30
    │   ┌── 25
    └── 20
        └── 10

Ref

https://zhuanlan.zhihu.com/p/152599308

https://blog.csdn.net/xiaojin21cen/article/details/97602146